比特幣時(shí)間冪律模型是什么?一文讀懂比特幣時(shí)間冪律模型。前物理學(xué)教授喬瓦尼·桑托斯塔西 (Giovanni Santostasi) 揭示了他預(yù)測(cè)比特幣價(jià)格的“冪律”模型——預(yù)測(cè)到 2045 年,每個(gè) BTC 的價(jià)值將達(dá)到 1000 萬(wàn)美元。 冪律是一種數(shù)學(xué)關(guān)系,其中一個(gè)值與另一個(gè)值的固定冪成正比。從地震頻率到股票市場(chǎng)變化的動(dòng)態(tài),冪律在各種自然發(fā)生的現(xiàn)象中都得到了觀察。

Santostasi 于 2018 年在 Reddit 的 r/Bitcoin 子版塊中首次分享了冪律模型。然而,在 YouTube 金融博主 Andrei Jeikh 在向他的 230 萬(wàn)訂閱者發(fā)布的視頻中提及該模型后,該模型在今年 1 月再次興起。Santostasi 表示,該模型預(yù)測(cè)比特幣可能會(huì)在 2026 年 1 月達(dá)到 210,000 美元的峰值,然后跌至 60,000 美元。
在 3 月 2 日與數(shù)學(xué)家和比特幣投資者 Fred Krueger的討論中,Santostasi 表示,冪律模型顯示了更容易理解和預(yù)測(cè)的長(zhǎng)期比特幣價(jià)格走勢(shì)模型。相比之下,主流媒體使用的大多數(shù)短期比特幣價(jià)格圖表往往顯示出對(duì)比特幣價(jià)格走勢(shì)的“混亂”和不準(zhǔn)確的看法。
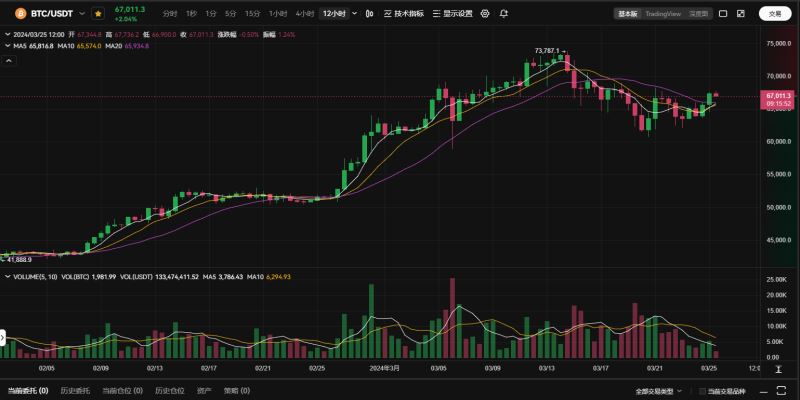
“但是什么時(shí)候你觀察 y 軸的對(duì)數(shù),你就會(huì)開(kāi)始看到那里的一些規(guī)律性,它看起來(lái)并不那么混亂,它看起來(lái)像是一個(gè)非常好的模式,”他解釋道。
桑托斯塔西表示,與現(xiàn)在廣受批評(píng)的存量-流量模型不同,冪律是對(duì)數(shù)而不是指數(shù)。
這意味著比特幣的價(jià)格不必隨著時(shí)間的推移不斷上漲,并且在該模型下仍然可以解釋最近在 2020 年至 2023 年期間出現(xiàn)的價(jià)格大幅波動(dòng)。
在 3 月 3 日發(fā)布的 X后續(xù)帖子中,克魯格概述了冪律應(yīng)用于比特幣時(shí)的進(jìn)一步數(shù)學(xué)模型,該模型預(yù)測(cè)比特幣的價(jià)格將在未來(lái)兩年內(nèi)達(dá)到 10 萬(wàn)美元。
克魯格的冪律模型預(yù)測(cè)到 2045 年比特幣價(jià)格將達(dá)到 1000 萬(wàn)美元。
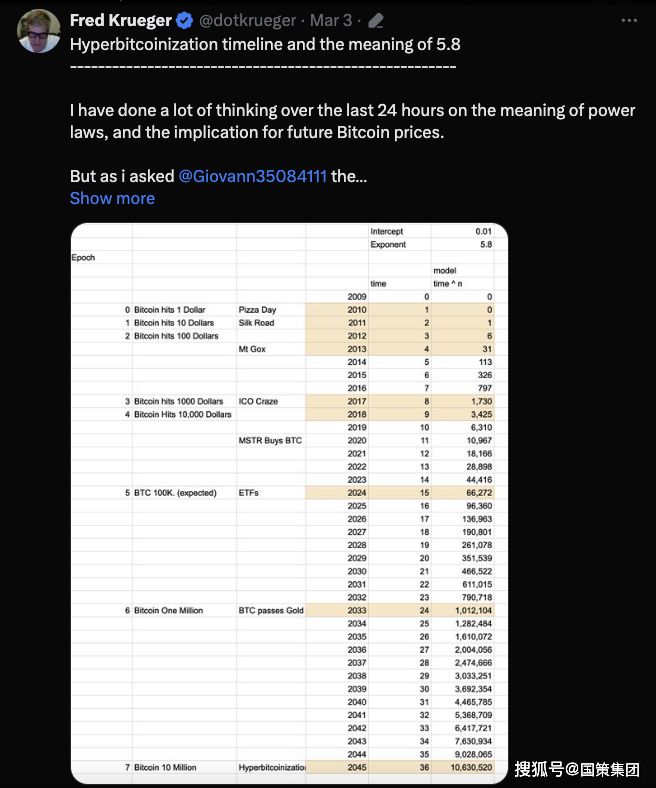
Krueger 補(bǔ)充說(shuō),如果比特幣遵循冪律模型,到 2033 年,其市值將超過(guò)黃金,屆時(shí)每個(gè)代幣的價(jià)值將達(dá)到 100 萬(wàn)美元。
盡管桑托斯塔西和克魯格相信冪律模型,但批評(píng)者表示,任何數(shù)學(xué)模型都可能容易出現(xiàn)重大錯(cuò)誤,并且無(wú)法考慮可能對(duì)價(jià)格產(chǎn)生嚴(yán)重影響的隨機(jī)事件。
比特幣基于時(shí)間的冪律,最初由 Giovanni Santostasi 于 2014 年提出,我們于 2019 年重新表述(作為走廊或三參數(shù)模型),描述了比特幣價(jià)格與時(shí)間之間的關(guān)系。具體來(lái)說(shuō),該模型描述了比特幣創(chuàng)世區(qū)塊之后的天數(shù)對(duì)數(shù)與比特幣美元價(jià)格對(duì)數(shù)之間的線性關(guān)系。
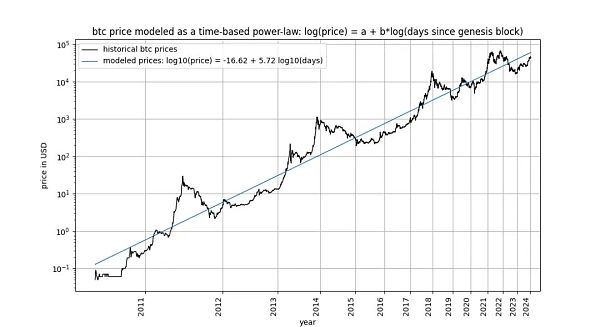
該模型吸引了包括 Marcel Burger、Tim Stolte 和 Nick Emblow 在內(nèi)的多位批評(píng)家,他們各自撰文對(duì)該模型進(jìn)行了 "反駁"。在本文中,我們將逐一剖析這三個(gè)批評(píng)中的一個(gè)關(guān)鍵論點(diǎn):時(shí)間與價(jià)格之間不存在協(xié)整性(cointegration)的說(shuō)法,認(rèn)為該模型 "無(wú)效",只是表明了一種虛假的關(guān)系。
真的是這樣嗎?
在本文中,我們將對(duì)這一問(wèn)題進(jìn)行深入研究。這使我們認(rèn)定,嚴(yán)格來(lái)說(shuō),協(xié)整不可能存在于時(shí)間相關(guān)模型中,包括我們自己的模型。然而,不可否認(rèn)的是,協(xié)整所必需的統(tǒng)計(jì)屬性之一在基于時(shí)間的冪律模型中是存在的。因此,我們得出結(jié)論認(rèn)為,基于時(shí)間的冪律模型在狹義上是協(xié)整的,我們的批評(píng)是錯(cuò)誤的,該模型是完全有效的。我們證明,這一結(jié)論同樣適用于“存量增量比”(S2F)模型,以及在長(zhǎng)期股票市場(chǎng)指數(shù)價(jià)格中觀察到的指數(shù)增長(zhǎng)。

隨機(jī)過(guò)程涉及隨機(jī)變量。隨機(jī)變量的值不是預(yù)先確定的。與此相反,確定性過(guò)程可以提前精確預(yù)測(cè) —— 它的方方面面都是事先已知的。股票市場(chǎng)價(jià)格等屬于隨機(jī)變量,因?yàn)槲覀儫o(wú)法提前預(yù)測(cè)資產(chǎn)的價(jià)格。因此,我們將股票或比特幣價(jià)格等時(shí)間序列視為隨機(jī)變量的觀測(cè)值。
相反,時(shí)間的流逝遵循確定性模式。每秒鐘都有一秒鐘過(guò)去,不存在任何不確定性。因此,事件發(fā)生后的持續(xù)時(shí)間是一個(gè)確定變量。
在研究協(xié)整之前,我們先來(lái)看看協(xié)整的基礎(chǔ)概念:平穩(wěn)性(stationary):
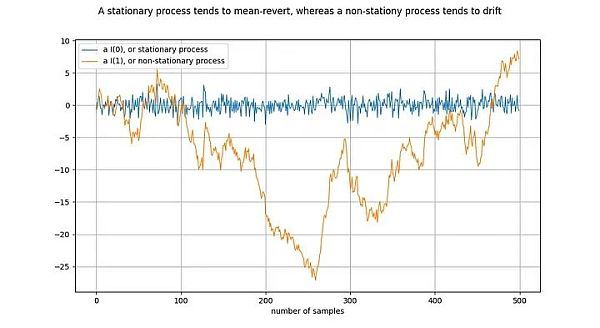
圖釋:將橙線差分一次,就得到了藍(lán)線。對(duì) I(1)時(shí)間序列差分一次,就得到了 I(0)時(shí)間序列。
平穩(wěn)過(guò)程(stationary process)是一種隨機(jī)過(guò)程(stochastic process),從廣義上講,它在一段時(shí)間內(nèi)具有相同的性質(zhì)。例如,對(duì)于平穩(wěn)過(guò)程來(lái)說(shuō),其均值和方差是確定和穩(wěn)定的。靜止時(shí)間序列的同義詞是 I(0)。源于平穩(wěn)過(guò)程的時(shí)間序列不應(yīng)該“漂移”(drift),而應(yīng)該趨向于平均值,通常是零值。
非平穩(wěn)過(guò)程的一個(gè)例子就是隨機(jī)漫步,例如物理學(xué)中的布朗運(yùn)動(dòng)或粒子擴(kuò)散:隨機(jī)漫步中的每個(gè)新值都取決于前一個(gè)值加上一個(gè)隨機(jī)數(shù)。非平穩(wěn)過(guò)程的屬性(如均值和方差)會(huì)隨時(shí)間而改變,或者沒(méi)有定義。非平穩(wěn)過(guò)程為 I(1)或更高,但通常為 I(1)。源于非平穩(wěn)過(guò)程的時(shí)間序列會(huì)隨著時(shí)間的推移而“漂移”,即傾向于偏離任何固定值。
符號(hào) I(1) 指的是一個(gè)時(shí)間序列需要“差分”(differenced)多少次才能達(dá)到靜態(tài)。差分是指求取時(shí)間序列中的值與其前值之間的差值。這大致相當(dāng)于求導(dǎo)數(shù)。平穩(wěn)時(shí)間序列已經(jīng)是平穩(wěn)的 —— 它需要經(jīng)過(guò) 0 次差分變成平穩(wěn)的,因此它是 I(0)。I(1)時(shí)間序列需要經(jīng)過(guò)一次差分才能達(dá)到平穩(wěn)。
上圖的繪制方式是,通過(guò)對(duì)橙色時(shí)間序列進(jìn)行一次差分,得到藍(lán)色時(shí)間序列。等價(jià)地,橙色時(shí)間序列是通過(guò)對(duì)藍(lán)色時(shí)間序列進(jìn)行積分得到的。
單位根過(guò)程(unit root process)指的是自回歸模型(autoregressive models)(更準(zhǔn)確地說(shuō)是 AR(1) 類型),其 rho 參數(shù)被估計(jì)為等于 1。雖然我們可以交替使用 rho 和根,但 rho 指的是過(guò)程的真實(shí)值,而這個(gè)值通常是未知的,需要進(jìn)行估計(jì)。估計(jì)結(jié)果就是“根”值。
rho 的值表示進(jìn)程對(duì)先前值的記憶程度。u 的值指的是誤差項(xiàng),假定為白噪聲。
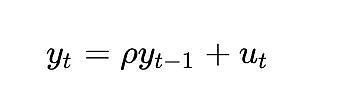
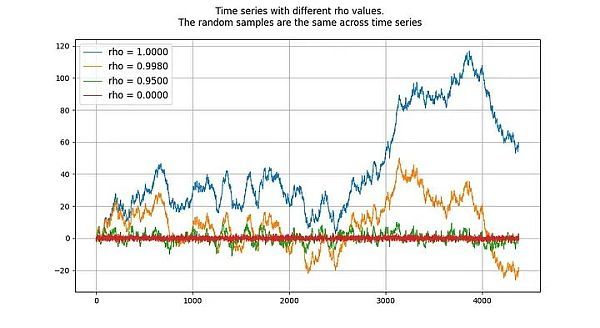
單位根過(guò)程是隨機(jī)游走過(guò)程,屬于非平穩(wěn)過(guò)程。“根”或 rho 值低于 1 的過(guò)程往往不會(huì)漂移,因此是平穩(wěn)的。即使是接近(但低于)1 的值,從長(zhǎng)期來(lái)看也傾向于均值回歸(而不是漂移)。因此,單位根過(guò)程的特殊性在于它與根值非常接近 1 的過(guò)程有著本質(zhì)的不同。
兩個(gè)隨機(jī)變量(本例中為時(shí)間序列)之間存在或不存在協(xié)整性(協(xié)整關(guān)系)。要使這對(duì)變量具有協(xié)整關(guān)系,兩者必須具有相同的積分階次,并且都是非平穩(wěn)的。此外(這是關(guān)鍵部分),兩個(gè)時(shí)間序列的線性組合必須是平穩(wěn)的。
如果兩個(gè)時(shí)間序列是非平穩(wěn)的,那么線性組合(在這種情況下,我們只需選擇兩個(gè)時(shí)間序列的差值)通常也是非平穩(wěn)的:
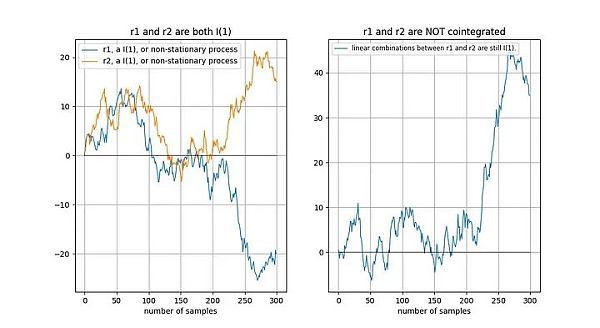
如果兩個(gè)非平穩(wěn)時(shí)間序列在長(zhǎng)期內(nèi)“以同樣的方式”漂移,那么線性組合(這里我們選擇 r2-0.5*r1)可能是平穩(wěn)的:
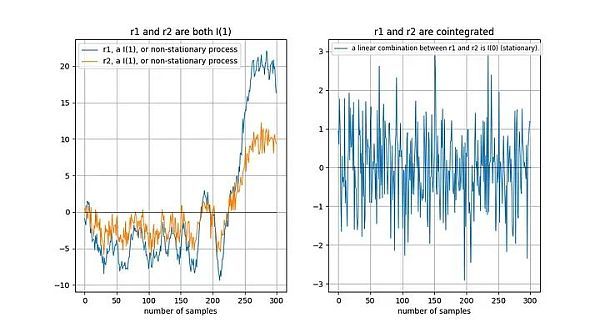
Tu 等人[1]直觀地描述了協(xié)整關(guān)系:
"時(shí)間序列之間存在協(xié)整關(guān)系意味著它們?cè)陂L(zhǎng)期內(nèi)具有共同的隨機(jī)漂移"。
為什么兩個(gè)非平穩(wěn)時(shí)間序列的線性組合是平穩(wěn)的?假設(shè)我們有兩個(gè)時(shí)間序列 x 和 y,我們?cè)噲D根據(jù) x 建立 y 模型:y = a + b*x。我們的模型誤差由 x 和 y 的線性組合給出:模型誤差 error = y - a - b*x 。我們希望模型誤差是平穩(wěn)的,即不會(huì)長(zhǎng)期漂移。如果模型誤差長(zhǎng)期漂移,那就意味著我們的模型不好,不能做出準(zhǔn)確的預(yù)測(cè)。
在 Engle 和 Granger [2](Granger 是協(xié)整概念的發(fā)明者,曾獲 2003 年諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng))的協(xié)整與誤差修正:表示、估計(jì)和檢驗(yàn)一文中,定義了協(xié)整的關(guān)鍵概念和檢驗(yàn)方法。該論文的關(guān)鍵是假設(shè)時(shí)間序列是隨機(jī)的,沒(méi)有確定性成分(我們稍后再談)。

如果存在確定性趨勢(shì),則應(yīng)在分析前將其去除:

在基于時(shí)間的冪律中,我們有兩個(gè)變量:
1. log_time:創(chuàng)世區(qū)塊之后天數(shù)的對(duì)數(shù)
2. log_price:價(jià)格的對(duì)數(shù)
根據(jù) Engle 和 Granger 的定義,兩個(gè)變量都必須是隨機(jī)變量,沒(méi)有確定性成分,而且必須是非平穩(wěn)的。此外,我們必須能夠找到這兩個(gè)變量的靜態(tài)線性組合。否則,這兩個(gè)變量之間就不存在協(xié)整關(guān)系。
在深入探討細(xì)節(jié)之前,讓我們先展示幾張模型數(shù)據(jù)本身的圖表,其中不包含任何平穩(wěn)或協(xié)整概念。請(qǐng)注意,基于時(shí)間的冪律產(chǎn)生的擬合效果直觀看來(lái)相當(dāng)不錯(cuò)。殘差向量(residuals vector)并沒(méi)有立即顯示出漂移。
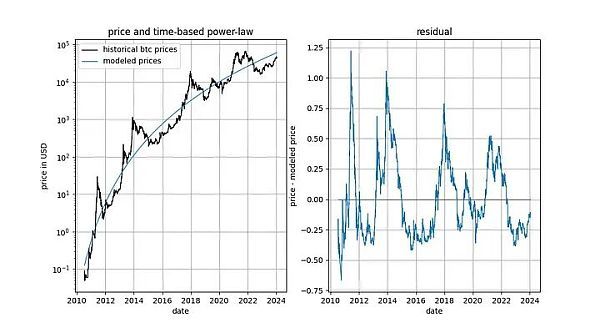
此外,該模型還顯示出卓越的樣本外性能(見(jiàn)下文)。出色的樣本外性能并不意味著該模型是虛假的 —— 基于虛假相關(guān)性的模型應(yīng)該只是虛假的,即無(wú)法準(zhǔn)確預(yù)測(cè)。檢驗(yàn)樣本外性能的方法是在有限的數(shù)據(jù)量(截至某個(gè)日期)上擬合模型,并對(duì)模型未擬合的時(shí)間段進(jìn)行預(yù)測(cè)(類似于交叉驗(yàn)證)。在樣本外期間,觀察到的價(jià)格經(jīng)常與建模價(jià)格交叉,觀察到的價(jià)格的最大偏離也沒(méi)有系統(tǒng)性地進(jìn)一步遠(yuǎn)離建模價(jià)格。
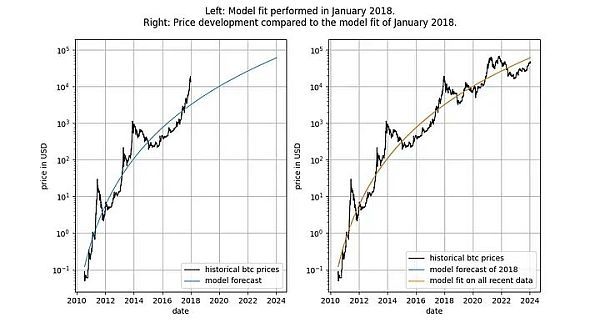
我們可以更加嚴(yán)格,觀察模型發(fā)布之后(2019 年 9 月)的表現(xiàn),因?yàn)槟P桶l(fā)布后,我們不可能有任何作弊行為 —— 我們不能事后更改模型。
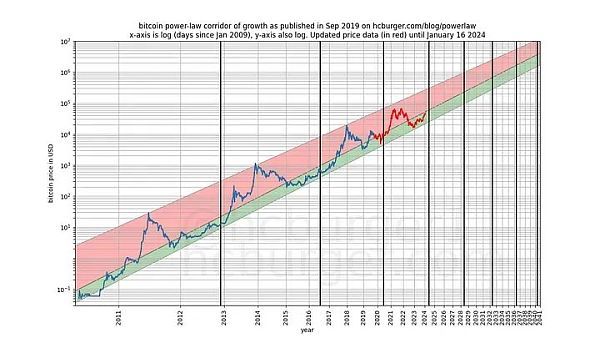
如果有人指責(zé)該模型只是基于一種虛假的相關(guān)性,那么該模型的預(yù)測(cè)能力應(yīng)該已經(jīng)讓人感到懷疑了。
要使 log_time 和 log_price 之間可能存在協(xié)整關(guān)系,這兩個(gè)變量必須是同階隨機(jī)變量,且至少是 1 階隨機(jī)變量。
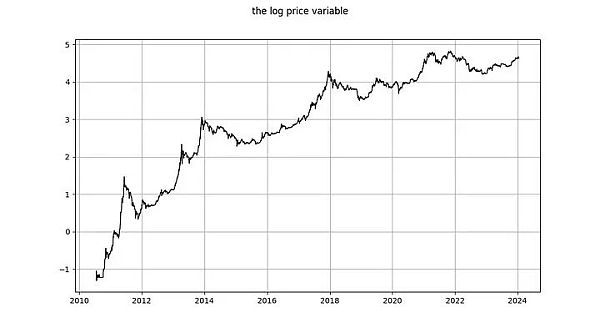
log_price 是平穩(wěn)時(shí)間序列嗎?Nick 使用未指定類型的 ADF 檢驗(yàn)(非平穩(wěn)性檢驗(yàn))和 KPSS 檢驗(yàn)(平穩(wěn)性檢驗(yàn))得出結(jié)論,log(price) 毫無(wú)疑問(wèn)是非平穩(wěn)的,因此是 I(1)或更高。Marcel Burger 通過(guò)目測(cè)得出結(jié)論,它是 I(1)。Tim Stolte 提出了一個(gè)更有趣的觀察:他對(duì)不同時(shí)期進(jìn)行了 ADF 檢驗(yàn)(未指定類型),并指出情況并非一目了然:“因此,我們無(wú)法堅(jiān)定地拒絕非平穩(wěn)性,并得出 log-price 存在非平穩(wěn)性跡象的結(jié)論。”
讓我們自己跑一下分析。與 Tim Stolte 類似,我們將在不同的時(shí)間窗口進(jìn)行 ADF 檢驗(yàn):總是從第一個(gè)可用日期開(kāi)始,每天增加一天(我們使用每日數(shù)據(jù))。這樣,我們就能看到 ADF 檢驗(yàn)的結(jié)果是如何隨時(shí)間變化的。但與 Tim 和 Nick 不同的是,我們要指定運(yùn)行哪個(gè)版本的 ADF 檢驗(yàn)。根據(jù)維基百科,DF 和 ADF 檢驗(yàn)有三種主要類型:

這三個(gè)版本的區(qū)別在于它們能夠適應(yīng)(移除)不同的趨勢(shì)。這與 Engle 和 Granger 要求去除任何確定性趨勢(shì)有關(guān) —— 這三個(gè)版本能夠去除三種簡(jiǎn)單的確定性趨勢(shì)類型。第一個(gè)版本試圖只使用過(guò)去的 log_price 數(shù)據(jù)來(lái)描述每日的 log_price 變化。第二個(gè)版本允許使用常數(shù)項(xiàng),其效果是 log_price 可以具有線性趨勢(shì)(向上或向下)。第三個(gè)版本允許二次方(拋物線)成分。
我們不知道 Tim 和 Nick 運(yùn)行的是哪個(gè)版本,但我們將運(yùn)行所有三個(gè)版本。
我們?cè)?ADF 檢驗(yàn)中使用的最大滯后期為 1,但使用更長(zhǎng)的滯后期不會(huì)對(duì)我們的結(jié)果和結(jié)論產(chǎn)生有意義的改變。我們將使用 python 的 statsmodels.tsa.stattools.adfuller 函數(shù),"maxlag"為 1,"regression"參數(shù)使用 "n"、"c "和 "ct"(相當(dāng)于維基百科上面描述的三種類型)。在下圖中,我們顯示了測(cè)試返回的 p 值(統(tǒng)計(jì)顯著性的衡量標(biāo)準(zhǔn)),p 值越小,表示平穩(wěn)的可能性越大(通常使用的臨界值為 0.05)。
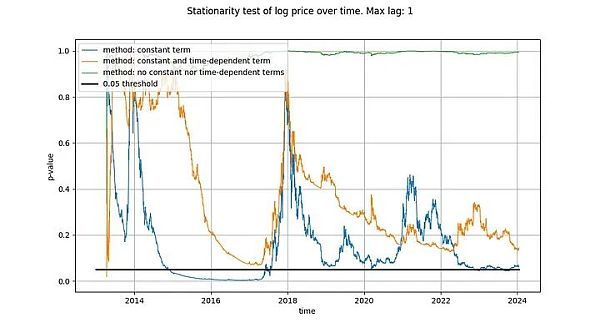
我們注意到,第一種方法(綠線)得出的結(jié)論是,log_price 時(shí)間序列是非平穩(wěn)的。第三種檢驗(yàn)方法(橙色線)的結(jié)論相同,但不那么果斷。有趣的是,允許常數(shù)項(xiàng)的檢驗(yàn)(藍(lán)線)無(wú)法判定時(shí)間序列是否平穩(wěn)(很可能 Tim 也使用了帶有常數(shù)項(xiàng)的 ADF 檢驗(yàn))。為什么這三個(gè)版本有如此大的差異,特別是為什么帶有常數(shù)項(xiàng)的版本不能排除 log_price 是平穩(wěn)的?
只有一種解釋:在 log_price 差分中僅使用常數(shù)項(xiàng)(導(dǎo)致 log_price 中的線性項(xiàng))可以“很好地”擬合時(shí)間序列,從而產(chǎn)生看起來(lái)幾乎是平穩(wěn)的殘差信號(hào)(盡管起點(diǎn)和終點(diǎn)的偏差相當(dāng)大)。完全不在 log_price 中使用確定性趨勢(shì),或使用二次項(xiàng)確定性效應(yīng),效果都遠(yuǎn)不如前者。
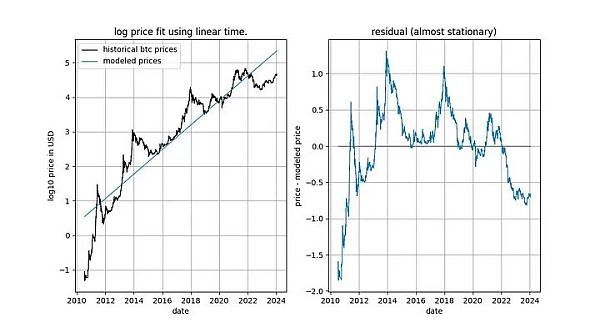
這已經(jīng)給了我們一個(gè)強(qiáng)烈的暗示,即時(shí)間與 log_price 之間存在關(guān)系。事實(shí)上,如果使用常數(shù)項(xiàng)進(jìn)行的 ADF 檢驗(yàn)得出的結(jié)論是信號(hào)是平穩(wěn)的,這就意味著線性時(shí)間項(xiàng)能夠很好地近似 log_price,從而得到平穩(wěn)的殘差。獲得平穩(wěn)的殘差是可取的,因?yàn)樗欠翘摷訇P(guān)系的標(biāo)志(即我們找到了正確的解釋變量)。線性時(shí)間趨勢(shì)并不完全符合我們的要求,但我們似乎正在接近它。
我們的結(jié)論與 Marcel Burger 的結(jié)論明顯不同,他(在另一篇文章中)說(shuō):
“在之前的分析中,我表明比特幣的價(jià)格是一階整合的,這一點(diǎn)仍然有效。比特幣在價(jià)格隨時(shí)間演變的過(guò)程中并沒(méi)有表現(xiàn)出任何確定性因素。”
我們的結(jié)論是,線性時(shí)間并不能充分解釋比特幣的價(jià)格隨時(shí)間變化的行為,但 log_price 有一個(gè)確定的時(shí)間因素是絕對(duì)清楚的。此外,在去除適當(dāng)?shù)拇_定性成分后(如 Engle 和 Granger 所要求的),也不清楚 log_price 是否為 I(1)。相反,它似乎是趨勢(shì)平穩(wěn)的,但仍需找到適當(dāng)?shù)拇_定性成分。
如果我們要尋找協(xié)整關(guān)系,log_price 不是 I(1)就已經(jīng)是個(gè)問(wèn)題了,因?yàn)橐箖蓚€(gè)變量協(xié)整,它們必須都是 I(1)或更高。
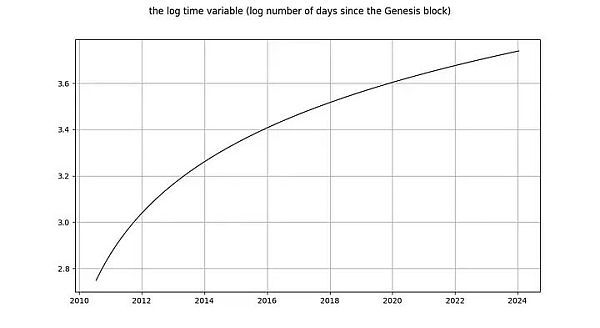
現(xiàn)在讓我們看看 log_time 變量。Marcel Burger 的結(jié)論是,log_time 似乎進(jìn)行了 6 階積分(他一直在進(jìn)行差分,直到遇到數(shù)值問(wèn)題)。他期望像對(duì)數(shù)這樣的數(shù)學(xué)函數(shù)能從一個(gè)完全確定的變量轉(zhuǎn)化為一個(gè)隨機(jī)變量,這種做法是毫無(wú)道理的。
Nick 對(duì) log_time 的結(jié)論與對(duì) log_price 變量的結(jié)論相同:毫無(wú)疑問(wèn),它是非平穩(wěn)的,因此 I(1) 或更高。Tim Stolte 聲稱 log_time 在構(gòu)造上是非平穩(wěn)的。這些說(shuō)法都令人吃驚!積分階次和協(xié)整是指隨機(jī)變量的概念,其中任何確定性趨勢(shì)都已被剔除(見(jiàn)上文 Engle 和 Granger [2])。需要提醒的是:確定性變量的值是預(yù)先知道的,而隨機(jī)變量的值是不知道的。時(shí)間(顯然)是完全確定的,對(duì)數(shù)函數(shù)也是完全確定的,因此 log_time 也是完全確定的。
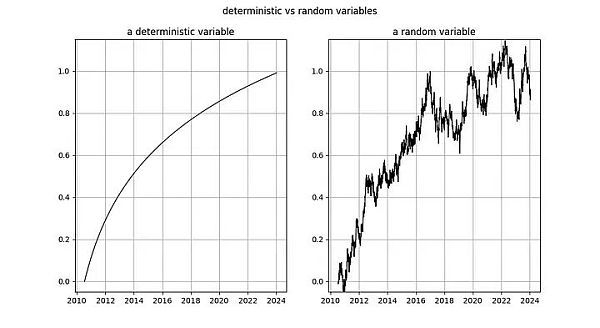
圖釋:左圖:自創(chuàng)世區(qū)塊之后的天數(shù)的對(duì)數(shù)是完全確定性的。右圖:隨機(jī)變量(看起來(lái)有點(diǎn)像左邊的確定性變量)。
如果我們按照 Engle 和 Granger 的方法,從 log_time 中移除確定性趨勢(shì),那么剩下的就是一個(gè)零向量,因?yàn)?log(x) - log(x) = 0,也就是說(shuō),我們?nèi)匀挥幸粋€(gè)完全確定的信號(hào)。這意味著我們陷入了困境 —— 我們無(wú)法將 log_time 這個(gè)完全確定的變量轉(zhuǎn)化為隨機(jī)變量,因此我們無(wú)法使用 Engle 和 Granger 的框架。
要想知道完全確定的變量在協(xié)整分析中會(huì)有多大問(wèn)題,還有一種方法,那就是考慮 Dickey-Fuller 檢驗(yàn)等平穩(wěn)性檢驗(yàn)如何處理它。讓我們考慮最簡(jiǎn)單的情況(其中 y 是感興趣的變量,rho 是需要估計(jì)的系數(shù),u 是假定為白噪聲的誤差項(xiàng)):
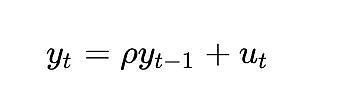
會(huì)發(fā)生什么?誤差項(xiàng) u_{t} 在所有 t 值中都為 0,因?yàn)槲覀儧](méi)有隨機(jī)成分 —— 應(yīng)該不需要誤差。但由于 log_time 是時(shí)間的非線性函數(shù),因此 rho 的值也必須取決于時(shí)間。
對(duì)于隨機(jī)變量來(lái)說(shuō),這個(gè)模型更有用,因?yàn)樽兞?rho 可以捕捉到之前的隨機(jī)值在多大程度上被記住了。但如果沒(méi)有隨機(jī)值,這個(gè)模型就沒(méi)有意義了。
對(duì)于確定性變量,其他類型的檢驗(yàn)也存在同樣的問(wèn)題。
因此,完全確定性變量不屬于協(xié)整分析的范疇。或者換一種說(shuō)法:協(xié)整分析不適用于確定性信號(hào),如果其中一個(gè)信號(hào)是確定性的,那么協(xié)整分析就是一種聲稱存在虛假關(guān)系的不合時(shí)宜的工具。
只有兩個(gè)變量都是 I(d),且 d 至少等于 1 的情況下,才存在協(xié)整關(guān)系。我們已經(jīng)證明 log_time 是一個(gè)完全確定的變量,不能用于靜態(tài)檢驗(yàn)。我們無(wú)法判斷 log_time 是 I(0)、I(1) 還是 I(6)。此外,log_price 也不是 I(1),而是趨勢(shì)平穩(wěn)的。
log_time 和 log_price 之間不存在協(xié)整關(guān)系,這是否意味著基于時(shí)間的冪律在統(tǒng)計(jì)上是無(wú)效的或虛假的?
當(dāng)然不是
在任何適當(dāng)?shù)慕y(tǒng)計(jì)分析中,使用混合確定變量和趨勢(shì)平穩(wěn)變量都是完全正確的。協(xié)整并不像我們的批評(píng)者試圖讓人相信的那樣,是統(tǒng)計(jì)關(guān)系分析的中心點(diǎn)。
因此,協(xié)整分析是不可行的。但是,應(yīng)用于冪律模型的平穩(wěn)分析可能還有用武之地。讓我們進(jìn)一步探討這個(gè)問(wèn)題。
我們之所以首先對(duì)輸入變量進(jìn)行協(xié)整分析,是因?yàn)槲覀兿M业蕉叩钠椒€(wěn)線性組合。將一個(gè)確定性變量(log_time)和一個(gè)趨勢(shì)平穩(wěn)變量(log_price)進(jìn)行組合,從而得到一個(gè)平穩(wěn)變量,這從根本上說(shuō)是不可能的。因此,與其尋找嚴(yán)格意義上的協(xié)整關(guān)系,我們可以簡(jiǎn)單地對(duì)殘差進(jìn)行平穩(wěn)性檢驗(yàn)(因?yàn)闅埐钪皇莾蓚€(gè)輸入信號(hào)的線性組合)。如果殘差是平穩(wěn)的,那么即使我們沒(méi)有嚴(yán)格遵循 Engle-Granger 協(xié)整檢驗(yàn),我們也找到了一個(gè)平穩(wěn)的線性組合(這正是協(xié)整的目的)。
James G. MacKinnon [3] 在他的論文協(xié)整檢驗(yàn)的臨界值中正是這樣解釋的:如果已經(jīng)進(jìn)行了“協(xié)整回歸”(將 log_time 與 log_price 聯(lián)系起來(lái)的回歸),那么協(xié)整檢驗(yàn)(Engle-Granger 檢驗(yàn))與對(duì)殘差進(jìn)行的平穩(wěn)性檢驗(yàn)(DF 或 ADF 檢驗(yàn))是一回事:

MacKinnon 重復(fù)了這一說(shuō)法:如果連接 log_time 和 log_price 的參數(shù)是先驗(yàn)已知的,那么就可以跳過(guò) Engle-Granger 協(xié)整檢驗(yàn),轉(zhuǎn)而對(duì)殘差進(jìn)行三種常見(jiàn)類型之一的平穩(wěn)性檢驗(yàn)(DF 或 ADF 檢驗(yàn)):
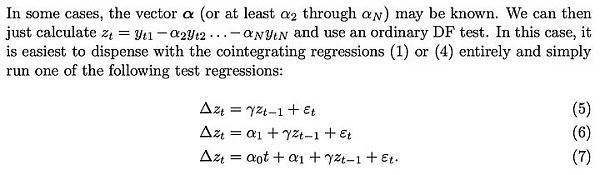
因此,我們可以使用兩種方法中的任何一種,除了得出的檢驗(yàn)統(tǒng)計(jì)量之外,這兩種方法是相同的:
1. 將 log_time 與 log_price 擬合,計(jì)算殘差(誤差)。根據(jù)殘差計(jì)算 DF,或者更好的是 ADF 檢驗(yàn)。由此得出的統(tǒng)計(jì)量可以說(shuō)明殘差是否平穩(wěn)。
2. 假設(shè) log_time 和 log_price 是 I(1),并運(yùn)行 Engel-Granger 協(xié)整檢驗(yàn)。得出的統(tǒng)計(jì)量也能說(shuō)明殘差是否平穩(wěn)。
對(duì)于 ADF 檢驗(yàn),我們使用 python 的 statsmodels.tsa.stattools.adfuller 函數(shù);對(duì)于 Engle-Granger 檢驗(yàn),我們使用 statsmodels.tsa.stattools.coint。對(duì)于這兩個(gè)函數(shù),我們都使用了不使用常數(shù)(不隨時(shí)間不斷漂移)的方式,因?yàn)槲覀兊臍埐畈粦?yīng)該包含隨時(shí)間不斷漂移(因?yàn)檫@意味著隨著時(shí)間的推移,模型開(kāi)始高估或低估價(jià)格)。
我們?cè)鴮懙溃珹DF 檢驗(yàn)和 Engle-Granger 檢驗(yàn)是等價(jià)的,但事實(shí)并非如此:它們不會(huì)產(chǎn)生相同的檢驗(yàn)統(tǒng)計(jì)量。Engle-Granger 協(xié)整檢驗(yàn)假設(shè)有 N=2 個(gè)隨機(jī)變量,而 ADF 檢驗(yàn)假設(shè)有 N=1 個(gè)隨機(jī)變量(N 是自由度的量度)。一個(gè)隨機(jī)變量可以受另一個(gè)隨機(jī)變量或一個(gè)確定變量的影響,但一個(gè)確定變量不能受一個(gè)隨機(jī)變量的影響。因此,在我們的案例中(只有一個(gè)確定變量 log_time),ADF 檢驗(yàn)(假定 N=1 個(gè)隨機(jī)變量)返回的統(tǒng)計(jì)量更可取。原則上,Engle-Granger 檢驗(yàn)和 ADF 檢驗(yàn)可能存在分歧,但在基于時(shí)間的模型中,實(shí)際情況并非如此。如下圖所示,結(jié)論是一樣的:我們得到了一個(gè)平穩(wěn)的殘差向量。兩種檢驗(yàn)的得分都遠(yuǎn)遠(yuǎn)低于 0.05 臨界值(表明殘差是平穩(wěn)的),而且長(zhǎng)期以來(lái)一直如此。
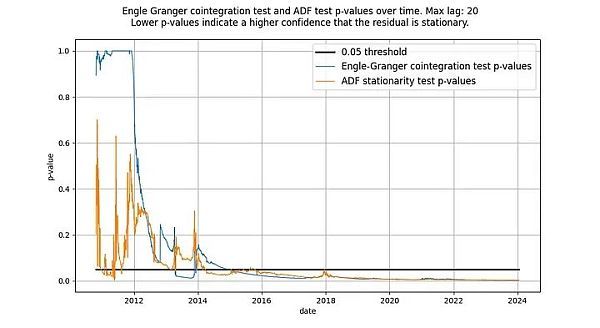
圖釋:根據(jù) ADF 和 Engle-Granger 檢驗(yàn),基于時(shí)間的冪律從 2016 年左右開(kāi)始具有平穩(wěn)的殘差。
兩種檢驗(yàn)最初都沒(méi)有顯示出平穩(wěn)的殘差是正常的。這是因?yàn)闅埐钚盘?hào)中的低頻成分會(huì)被誤認(rèn)為是非平穩(wěn)信號(hào)。只有隨著時(shí)間的推移,殘差的均值回歸才會(huì)變得明顯,實(shí)際上是平穩(wěn)的。
S2F 模型被普遍否定,似乎是因?yàn)閲?yán)格意義上的協(xié)整被證明是不可能的,其原因與基于時(shí)間的冪律相似:輸入變量是(部分)確定的。然而,該模型產(chǎn)生的殘差看起來(lái)非常平穩(wěn)。
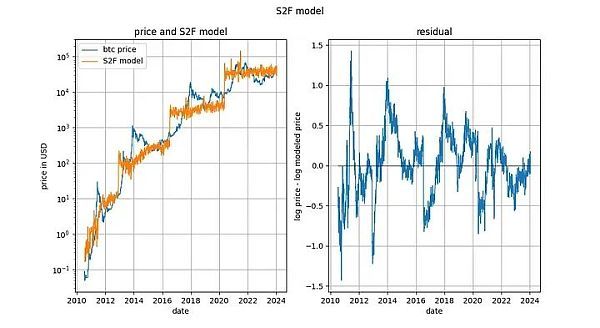
事實(shí)上,Engle-Granger 協(xié)整檢驗(yàn)和 ADF 平穩(wěn)性檢驗(yàn)(因?yàn)橛幸粋€(gè)確定變量和一個(gè)隨機(jī)變量,所以更可取)得出的 p 值都非常接近 0。因此,不應(yīng)以“缺乏協(xié)整性”(實(shí)際上是“缺乏平穩(wěn)性”)為由排除 S2F 模型。
然而,我們?cè)?2020 年初指出,還有其他跡象表明 S2F 模型不成立。我們預(yù)測(cè) BTCUSD 的價(jià)格將低于 S2F 模型的預(yù)測(cè),事實(shí)證明這一預(yù)測(cè)是有先見(jiàn)之明的。
觀察長(zhǎng)期股價(jià)指數(shù)與時(shí)間的對(duì)比也很有趣(此處為不含紅利再投資的標(biāo)準(zhǔn)普爾 500 指數(shù))。眾所周知,主要股票市場(chǎng)指數(shù)平均以 7% 左右的指數(shù)速度增長(zhǎng)。事實(shí)上,我們通過(guò)指數(shù)回歸也證實(shí)了這一點(diǎn)。
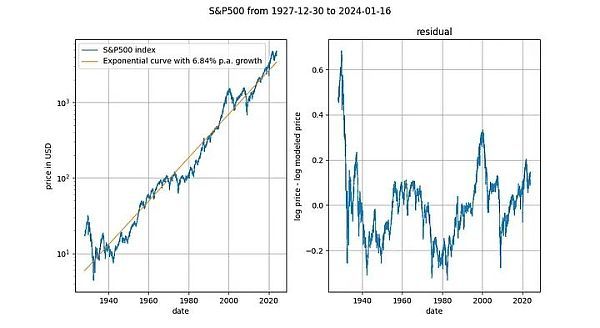
在這里,我們又遇到了一個(gè)確定性變量(時(shí)間)。Engle-Granger 協(xié)整檢驗(yàn)得出的 p 值約為 0.025,ADF 檢驗(yàn)(首選)得出的 p 值約為 0.0075(但這些值在很大程度上取決于選擇的確切時(shí)間段)。再一次,平穩(wěn)的殘差。股票價(jià)格的指數(shù)時(shí)間趨勢(shì)是有效的。
S2F 模型最初受到高度評(píng)價(jià)(尤其是 Marcel Burger 和 Nick Emblow),原因是該模型據(jù)稱具有良好的計(jì)量經(jīng)濟(jì)學(xué)基礎(chǔ),特別是存在協(xié)整關(guān)系。隨著潮流的轉(zhuǎn)變,S2F 模型顯然不存在嚴(yán)格意義上的協(xié)整關(guān)系,Marcel 和 Nick 都跳船了,宣布 S2F 模型無(wú)效。似乎在這一事件之后,大眾對(duì) S2F 模型的看法也發(fā)生了變化。Eric Wall 對(duì)事件的轉(zhuǎn)折做了一個(gè)極好的簡(jiǎn)短總結(jié)。
我們已經(jīng)解釋過(guò),而且計(jì)量經(jīng)濟(jì)學(xué)文獻(xiàn)(MacKinnon [3])也同意我們的觀點(diǎn),即協(xié)整性和平穩(wěn)性幾乎可以互換使用(統(tǒng)計(jì)量的值除外)。根據(jù)這一觀點(diǎn),我們認(rèn)為 S2F 模型在協(xié)整性/平穩(wěn)性方面沒(méi)有任何問(wèn)題,因此,因?yàn)樗^缺乏協(xié)整性而改變對(duì) S2F 模型的看法是錯(cuò)誤的。我們同意 S2F 模型是錯(cuò)誤的,但其錯(cuò)誤的原因不在于缺乏協(xié)整性。
比特幣的時(shí)間冪律模型因缺乏協(xié)整性而受到批評(píng),據(jù)說(shuō)這標(biāo)志著 log_time 和 log_price 之間的關(guān)系是虛假的。我們已經(jīng)證明,比特幣基于時(shí)間的冪律模型的殘差明顯是平穩(wěn)的,因此批評(píng)者的推理是值得商榷的。
比特幣的時(shí)間冪律模型是有效、穩(wěn)定和強(qiáng)大的。一如既往。
本文是譯自 Harold Christopher Burger 及 Peter Vijn 合作的論文比特幣的時(shí)間冪律模型及其協(xié)整性再探討(Bitcoin’s time-based power-law and cointegration revisited, 2024.1.31),理論性較強(qiáng),適合有一定統(tǒng)計(jì)學(xué)基礎(chǔ)的讀者閱讀。
關(guān)于所謂的時(shí)間冪律模型,教鏈在過(guò)去數(shù)載曾寫過(guò)多篇文章進(jìn)行介紹。
業(yè)內(nèi)有一位比較知名的匿名分析師PlanB一直比較推崇用S2F硬度來(lái)和價(jià)格進(jìn)行建模,這就是所謂的S2F模型。不過(guò)很可惜:S2F模型是錯(cuò)的。但請(qǐng)注意,這不代表S2F這個(gè)指標(biāo)沒(méi)有意義,只是說(shuō),S2F硬度的變化,與價(jià)格的關(guān)系,不像PlanB所描繪的那樣“激進(jìn)”。
下面這個(gè)圖就很清晰地展示了冪律模型和S2F模型的相對(duì)關(guān)系:
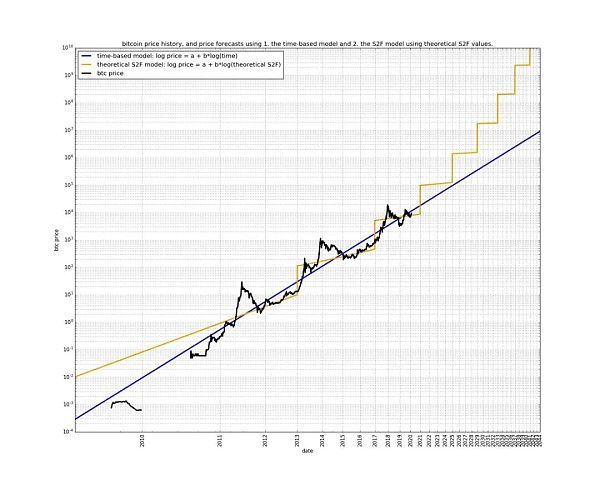
顯然,S2F模型認(rèn)為時(shí)間線性流逝就可以推動(dòng)價(jià)格的指數(shù)增長(zhǎng),而冪律模型則認(rèn)為時(shí)間的指數(shù)流逝才能推動(dòng)價(jià)格的指數(shù)增長(zhǎng)。
教鏈傾向于使用S2F硬度來(lái)形象化產(chǎn)量減半所導(dǎo)致的“相變”,但使用冪律模型把比特幣變換到雙對(duì)數(shù)空間中進(jìn)行線性回歸。冪律模型的優(yōu)雅特別有支持向量機(jī)(SVM)的神韻,所以甚合我意。
下面,就是 H. Burger & P. Vijn 的論文。Enjoy!
你已經(jīng)迷失方向了嗎?也許你對(duì)“協(xié)整性”一詞并不熟悉?別擔(dān)心:因果推論和非虛假關(guān)系領(lǐng)域的專家、為什么之書的作者 Judea Pearl 聲稱自己對(duì)這個(gè)問(wèn)題一無(wú)所知。我們將努力充分闡明手頭的相關(guān)術(shù)語(yǔ)。
在推特上比特幣相關(guān)話題討論中,關(guān)于協(xié)整性的爭(zhēng)論非常有趣,而且相當(dāng)引人入勝。許多“存量增量比”和“冪律”的追隨者都感到困惑。有興趣的讀者可以通過(guò)搜索“什么是協(xié)整”來(lái)親眼目睹這一點(diǎn)。隨著時(shí)間的推移,一些貢獻(xiàn)者似乎已經(jīng)掌握并完善了他們的理解,而另一些貢獻(xiàn)者則仍然感到困惑、轉(zhuǎn)換陣營(yíng)或迷失方向。直到現(xiàn)在,我們才開(kāi)始關(guān)注這個(gè)話題。
相關(guān)閱讀推薦
最新資訊
最新游戲

擺渡人生:隱河市浮生記完整版
查看
誰(shuí)是小丑正版
查看
想要成為影之實(shí)力者官網(wǎng)版
查看
魔法之光內(nèi)購(gòu)版
查看
信任的進(jìn)化官方下載
查看
靈魂遠(yuǎn)征中文版
查看
別喂猴子最新版
查看
王者榮耀海外測(cè)試服
查看
WheelieChallenge最新版
查看熱門文章
熱門游戲

生化危機(jī)4 v1手機(jī)版
查看
地鐵酷跑
查看
食夢(mèng)計(jì)劃官方版
查看
植物大戰(zhàn)僵尸西游版 v40.10內(nèi)購(gòu)版
查看
游戲串不用錢免費(fèi)版 v2022無(wú)限時(shí)間版
查看
silly wisher v0.59正版
查看
寵物連連消(寵物連連看消除游戲) v1.4.8安卓版
查看
熱血英雄 v1.3.0
查看
老爹披薩店togo游戲
查看
易玩游戲盒子免費(fèi)修改版
查看
老爹意大利面店togo(Papa)
查看
我的安吉拉2 v25.2.1.3版本
查看
gacha cute最新版 v1.1.0
查看
異界修真手游 v1.1.1安卓版
查看
勇猛之路二戰(zhàn)正版 v2.53.1中文版
查看
流言偵探 v2.5.4
查看
浮島冒險(xiǎn)(Forager) v1.0.13
查看
鋼鐵戰(zhàn)隊(duì)安卓版塔防即時(shí)戰(zhàn)略游戲 v1.8.4官方版
查看